| Ligne 126 : | Ligne 126 : | ||
|Step_Picture_00=Exp_rimenter_les_saisons_Rayons2.jpg | |Step_Picture_00=Exp_rimenter_les_saisons_Rayons2.jpg | ||
|Step_Picture_01=Exp_rimenter_les_saisons_Incidences.jpg | |Step_Picture_01=Exp_rimenter_les_saisons_Incidences.jpg | ||
| + | }} | ||
| + | {{Tuto Step | ||
| + | |Step_Title=Quelques propositions d'animation | ||
| + | |Step_Content=Voici par exemple le conducteur que j'ai suivi dans mes animations: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Un article intéressant de wikipedia: https://fr.vikidia.org/wiki/R%C3%A9volution_de_la_Terre_autour_du_Soleil | ||
}} | }} | ||
{{Notes}} | {{Notes}} | ||
Version du 14 juillet 2020 à 19:45
Sommaire
- 1 Introduction
- 2 Video d'introduction
- 3 Étape 1 - Description du matériel
- 4 Étape 2 - Quelques détails du montage
- 5 Étape 3 - Connaissances de base
- 6 Étape 4 - Chronométrage des durées du jour et de la nuit
- 7 Étape 5 - Effet de l'inclinaison sur l'éclairement solaire
- 8 Étape 6 - Quelques propositions d'animation
- 9 Commentaires
Introduction
Bien que cette présentation décrive le matériel et la séquence pour faire une animation sur le thème du mouvement de la terre autour du soleil, un enfant de fin de primaire ou de collège pourrait tout à fait se fabriquer le matériel pour "expérimenter les saisons".
"Expérimenter les saisons"... qu'est-ce que c'est ?
C'est principalement se rendre compte de manière concrète de la durée des jours et de la variation de l'éclairement solaire tout au long d'une année où la terre fait son périple autour du soleil. De façon concrète les durées du jour et de la nuit seront chronométrées à différents moments importants de l'année (Été, Hiver et Équinoxes d'automne et de printemps).
Mp4
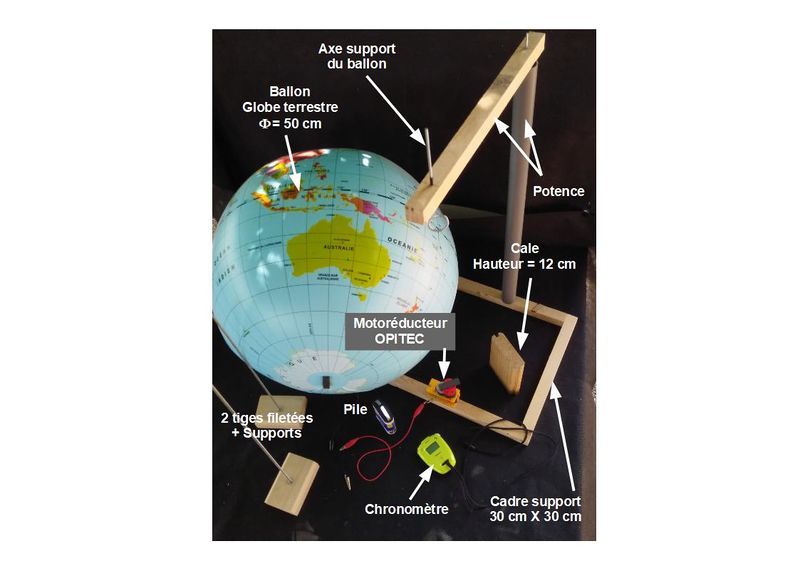
Étape 1 - Description du matériel
L'élément important est le ballon qui représente le globe terrestre.
On trouve différentes versions de globe gonflable de diamètre 50 cm, mais ce qui est important c'est que la valve de gonflage soit située au pôle nord. Il est également important que les pays soient à peu près bien représentés avec si possible leurs capitales. De même, fuseaux horaires et parallèles doivent être représentés.
Pour animer ce globe en rotation il faut également un support constitué d'une base carrée de 30 cm x 30 cm et d'une potence.
Sur la base du support est fixé un motoréducteur OPITEC qui supporte le globe par son pôle Sud et le fait tourner autour de son axe Nord-Sud. Au pôle Nord la valve de gonflage est retenue par une boucle qui se termine par un axe.
Dans la réalité, l'axe de la terre est incliné de 23° par rapport au plan de l'écliptique, ce qui est réalisé ici par une cale de hauteur 12 cm.
Pour l'expérimentation on a également besoin de repères figurant la séparation jour-nuit. C'est le rôle des deux tiges filetées de diamètre 4 mm fixées verticalement sur deux supports en bois.
Et enfin, le chronomètre qui permettra de mesurer les durées des jours et des nuits....
Étape 2 - Quelques détails du montage
La figure 1 montre le montage global avec la cale de 12 cm à l'avant, ce qui provoque l'inclinaison de l'axe de rotation du globe de 23°(figure 4), comme dans la réalité.
La figure 2 détaille le motoréducteur OPITEC avec sa fixation au ballon. Le réducteur doit être adapté pour que le globe fasse typiquement 1 tour par minute. Mais aucune valeur précise n'est requise. Dans notre cas par exemple la rotation s'effectue environ en 64 secondes. La figure 2 détaille également le couplage entre le motoréducteur et le ballon, au moyen de deux barreaux aimantés. Chaque barreau a une face collée avec du scotch double face. L'autre face sert à accoupler magnétiquement le ballon et le motoréducteur.
La figure 3 détaille l'accrochage de la valve du ballon dans une boucle qui se termine par un axe tournant dans un trou percé dans la potence. Le léger appui sur le ballon est réglé et fixé par un système écrou / contre-écrou.
Étape 3 - Connaissances de base
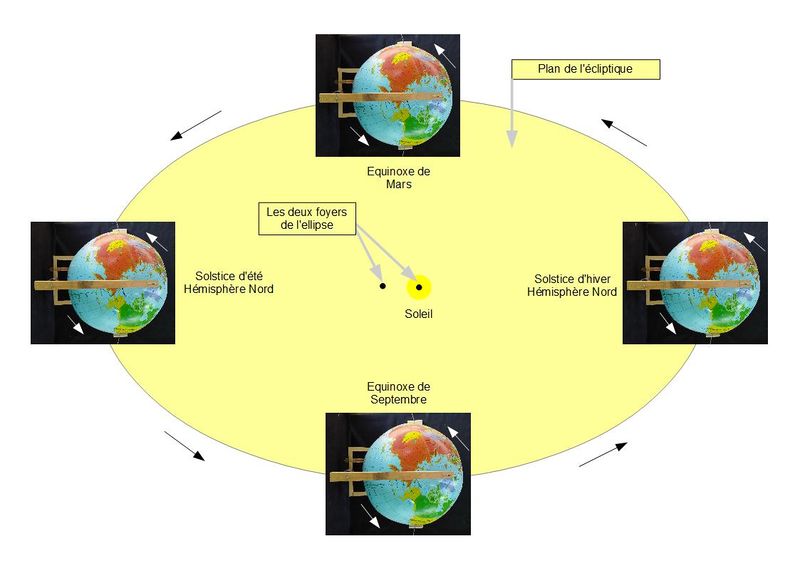
La trajectoire de la terre autour du soleil est une ellipse très peu aplatie. Elle a donc deux foyers assez proches dont l'un est l'emplacement du soleil. Le plan de cette ellipse est appelé plan écliptique car il est le lieu des éclipses de lune ou de soleil (...mais c'est une autre animation....)
La terre fait le tour de cette ellipse en un an. La distance entre la terre et le soleil varie assez peu au cours de cette révolution. Les distances sont considérables. La lumière du soleil met 8 minutes à nous parvenir (c = 300 000 Km /s) et la longueur de l'orbite sur l'ellipse est de 1 milliard de kilomètres.
Au cours de ce voyage d'un an la terre fait un tour sur elle-même chaque jour et effectue 365 tours sur elle-même pour parcourir l'ellipse. Au bout de cette année de 365 jours le cycle recommence à l'infini.
L'axe de rotation de la terre est incliné sur le plan de l'écliptique d'une valeur de 23°. La direction de cette inclinaison reste la même tout le long de l'année. La direction du basculement correspond à la direction du grand axe de l'ellipse. C'est cette inclinaison qui est à la base des saisons.
Les différentes saisons sont décrites sur la photo. On peut noter que pour l'hémisphère nord en été la distance au soleil est plus grande qu'en hiver, ce qui peut paraître paradoxal. En fait l'effet de cette petite variation de distance existe bien mais il est largement contrebalancé par les effets de l'inclinaison (voir video d'introduction).
Étape 4 - Chronométrage des durées du jour et de la nuit
Et voici que vient le mot que les enfants retiennent le mieux: le terminateur !
Le soleil produit un tube de rayons presque parallèles (0.5° de divergence), capables d'éclairer la terre entière (diamètre 13 000 Km). Bien sûr seul l'hémisphère faisant face au soleil est éclairé alors que l'autre est dans la nuit. La transition entre jour et nuit correspond à un grand cercle autour de la terre. C'est lui le terminateur.
Comme ce cercle est difficile à matérialiser pendant que la sphère tourne, on utilise deux tiges verticales qui définissent un plan passant par le centre de la sphère. L'intersection de ce plan avec la surface de la sphère correspond au cercle terminateur.
Pour le chronométrage il est important de voir passer les villes du jour à la nuit et inversement. Il suffit de placer un œil dans le plan défini par les deux tiges verticales.
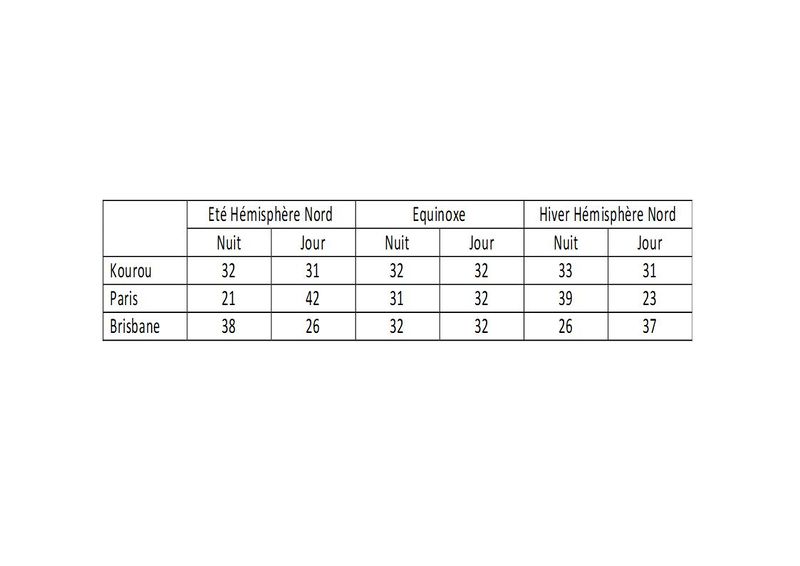
Il est alors facile de mesurer les durées relatives du jour et de la nuit pour n'importe quelle ville du globe et on peut établir un tableau comme celui de la figure 2. Dans la réalité la terre fait un tour sur elle-même en 24 Heures. Sur notre maquette la durée d'un tour est d'environ 64 secondes. Il suffit de faire la somme des durées des nuits et des jours: Pour n'importe quel point du globe la durée est bien de 64 secondes qui représentent en fait 24H.
On a considérablement accéléré le mouvement et c'est bien pratique pour expérimenter..... Par contre, ce qui est important, c'est que le ratio entre la durée du jour et de la nuit est conservé.
Étape 5 - Effet de l'inclinaison sur l'éclairement solaire
Les durées relatives du jour et de la nuit en fonction de la situation sur le globe ne sont qu'un contributeur des saisons. Un autre contributeur important est l'éclairement solaire en fonction de l'inclinaison des rayons sur le sol.
En photométrie, l'éclairement correspond à la puissance lumineuse tombant sur une surface unité. Elle s'exprime en Watts / m2.
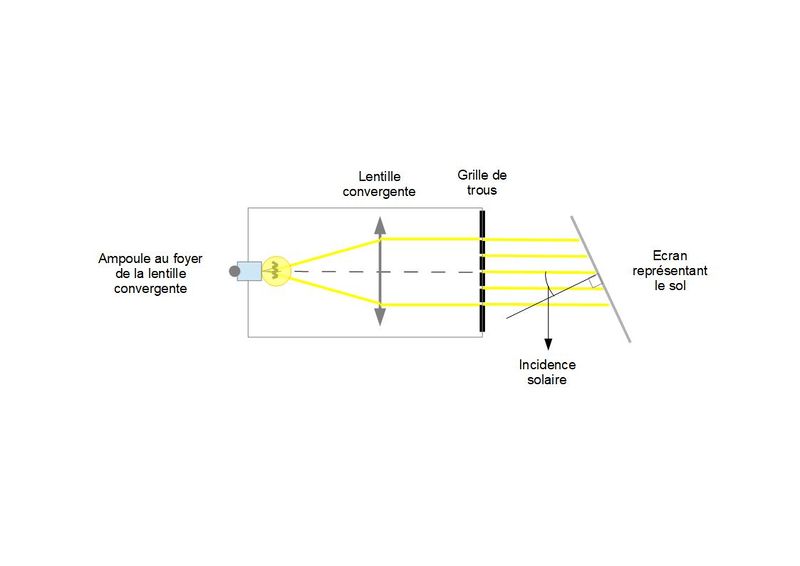
Pour visualiser cet effet on a réalisé une source de lumière collimatée (rayons parallèles) éclairant une grille de trous régulièrement espacés (figure 1).
Le soleil est évidemment une source de rayons contigus alors que notre source n'est qu'un échantillonnage espacé de ces rayons. Chacun de ces rayons transporte une certaine puissance élémentaire.
Avec notre source nous mesurerons l'éclairement solaire sur une surface tout simplement en comptant le nombre de rayons arrivant sur une surface unité.
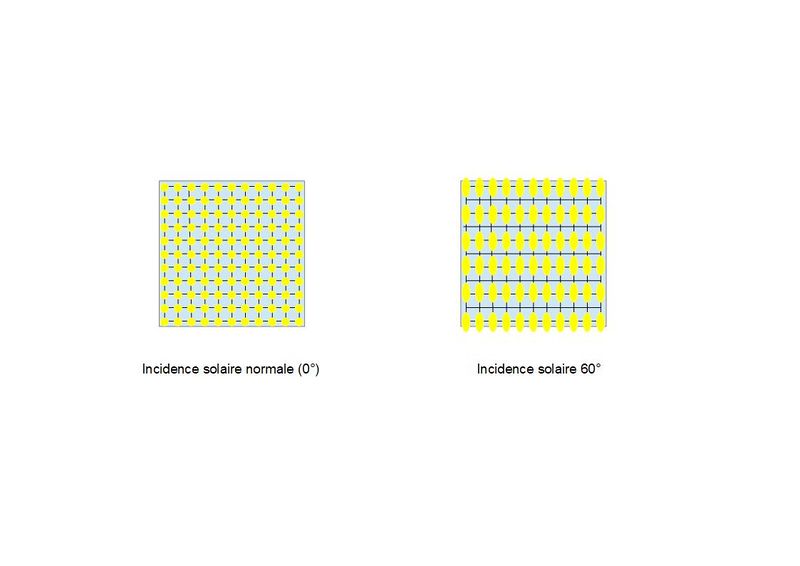
Sur la figure 2 on a représenté la comparaison entre une incidence solaire de 0° (incidence normale) et une incidence solaire de 60°. On constate que pour une incidence de 60°, le nombre de rayons incidents est divisé par deux, ce qui signifie que la puissance reçue par unité de surface est également divisée par deux.
On retrouve bien là la variation théorique de l'éclairement en fonction de l'incidence E = Eo x Cos (Incidence), sachant que Cos(60°) = 0.5
Étape 6 - Quelques propositions d'animation
Voici par exemple le conducteur que j'ai suivi dans mes animations:
Un article intéressant de wikipedia: https://fr.vikidia.org/wiki/R%C3%A9volution_de_la_Terre_autour_du_Soleil
Dernière modification 7/09/2021 par user:Occitan.
Published